Construct a Surjection G B ↀ™ 0; 1 Again Think About Digits

Properties of mathematical functions

	surjective	non-surjective
injective	bijective	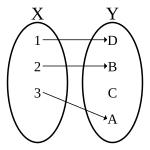injective-simply
not- injective	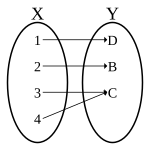surjective-only	full general

In mathematics, injections, surjections, and bijections are classes of functions distinguished by the mode in which arguments (input expressions from the domain) and images (output expressions from the codomain) are related or mapped to each other.

A function maps elements from its domain to elements in its codomain. Given a role ${\displaystyle f\colon X\to Y}$ :

• The office is injective, or one-to-one, if each chemical element of the codomain is mapped to by at about i element of the domain, or equivalently, if singled-out elements of the domain map to distinct elements in the codomain. An injective function is also called an injection.^[1] Notationally:

${\displaystyle \forall ten,x'\in X,f(x)=f(ten')\implies x=10',}$

or, equivalently (using logical transposition),

${\displaystyle \forall x,x'\in 10,10\neq x'\implies f(10)\neq f(x').}$ ^{[2] [3] [4]}

• The function is surjective, or onto, if each element of the codomain is mapped to by at least ane element of the domain. That is, the paradigm and the codomain of the role are equal. A surjective function is a surjection.^[one] Notationally:

${\displaystyle \forall y\in Y,\exists x\in 10{\text{ such that }}y=f(x).}$ ^{[ii] [3] [iv]}

• The function is bijective (one-to-1 and onto, one-to-1 correspondence, or invertible) if each element of the codomain is mapped to by exactly ane chemical element of the domain. That is, the function is both injective and surjective. A bijective function is also called a bijection.^{[1] [2] [3] [four]} That is, combining the definitions of injective and surjective,

${\displaystyle \forall y\in Y,\exists !x\in X{\text{ such that }}y=f(x),}$

where ${\displaystyle \exists !10}$ means "there exists exactly one x".

• In any example (for any function), the following holds:

${\displaystyle \forall x\in 10,\exists !y\in Y{\text{ such that }}y=f(x).}$

An injective function need not be surjective (non all elements of the codomain may be associated with arguments), and a surjective office demand not be injective (some images may be associated with more than than i argument). The iv possible combinations of injective and surjective features are illustrated in the adjacent diagrams.

Injection [edit]

Injective composition: the 2d part need not be injective.

A function is injective (1-to-one) if each possible element of the codomain is mapped to by at most one argument. Equivalently, a function is injective if it maps distinct arguments to distinct images. An injective function is an injection.^[1] The formal definition is the following.

The office ${\displaystyle f\colon X\to Y}$ is injective, if for all ${\displaystyle x,x'\in X}$ , ${\displaystyle f(x)=f(x')\Rightarrow 10=x'.}$ ^{[2] [3] [iv]}

The following are some facts related to injections:

Surjection [edit]

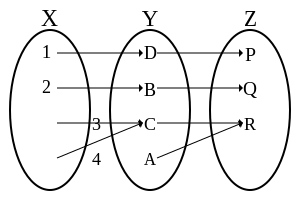
Surjective composition: the first function demand not be surjective.

A function is surjective or onto if each element of the codomain is mapped to past at least i chemical element of the domain. In other words, each element of the codomain has non-empty preimage. Equivalently, a function is surjective if its image is equal to its codomain. A surjective role is a surjection.^[1] The formal definition is the post-obit.

The function ${\displaystyle f\colon X\to Y}$ is surjective, if for all ${\displaystyle y\in Y}$ , in that location is ${\displaystyle x\in Ten}$ such that ${\displaystyle f(x)=y.}$ ^{[2] [3] [4]}

The following are some facts related to surjections:

• A function ${\displaystyle f\colon X\to Y}$ is surjective if and merely if it is correct-invertible, that is, if and only if there is a function ${\displaystyle one thousand\colon Y\to 10}$ such that ${\displaystyle f\circ g=}$ identity part on ${\displaystyle Y}$ . (This argument is equivalent to the precept of option.)
• By collapsing all arguments mapping to a given fixed paradigm, every surjection induces a bijection from a quotient set up of its domain to its codomain. More precisely, the preimages under f of the elements of the image of ${\displaystyle f}$ are the equivalence classes of an equivalence relation on the domain of ${\displaystyle f}$ , such that x and y are equivalent if and only they have the same epitome under ${\displaystyle f}$ . As all elements of any one of these equivalence classes are mapped by ${\displaystyle f}$ on the same element of the codomain, this induces a bijection between the quotient set by this equivalence relation (the ready of the equivalence classes) and the epitome of ${\displaystyle f}$ (which is its codomain when ${\displaystyle f}$ is surjective). Moreover, f is the composition of the approved projection from f to the quotient ready, and the bijection between the quotient set and the codomain of ${\displaystyle f}$ .
• The composition of two surjections is over again a surjection, but if ${\displaystyle g\circ f}$ is surjective, then it tin can only be ended that ${\displaystyle 1000}$ is surjective (see effigy).

Bijection [edit]

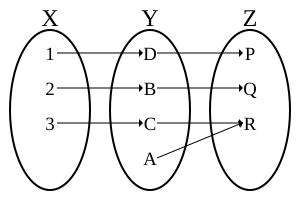
Bijective composition: the first role need not be surjective and the 2nd function need not exist injective.

A function is bijective if it is both injective and surjective. A bijective part is too called a bijection or a one-to-ane correspondence. A role is bijective if and just if every possible image is mapped to past exactly one argument.^[1] This equivalent condition is formally expressed as follow.

The function ${\displaystyle f\colon X\to Y}$ is bijective, if for all ${\displaystyle y\in Y}$ , at that place is a unique ${\displaystyle x\in X}$ such that ${\displaystyle f(x)=y.}$ ^{[ii] [3] [four]}

The following are some facts related to bijections:

Cardinality [edit]

Suppose that i wants to ascertain what it means for two sets to "have the same number of elements". One way to do this is to say that 2 sets "have the same number of elements", if and only if all the elements of one set can be paired with the elements of the other, in such a way that each element is paired with exactly 1 element. Accordingly, one can define two sets to "have the same number of elements"—if there is a bijection between them. In which instance, the ii sets are said to accept the aforementioned cardinality.

Likewise, one tin can say that set ${\displaystyle X}$ "has fewer than or the aforementioned number of elements" as fix ${\displaystyle Y}$ , if there is an injection from ${\displaystyle Ten}$ to ${\displaystyle Y}$ ; i can besides say that prepare ${\displaystyle Ten}$ "has fewer than the number of elements" in set ${\displaystyle Y}$ , if there is an injection from ${\displaystyle Ten}$ to ${\displaystyle Y}$ , but not a bijection between ${\displaystyle 10}$ and ${\displaystyle Y}$ .

Examples [edit]

It is important to specify the domain and codomain of each function, since by changing these, functions which announced to be the same may have different properties.

Injective and surjective (bijective)

The identity function id _Ten for every non-empty prepare 10, and thus specifically ${\displaystyle \mathbf {R} \to \mathbf {R} :x\mapsto x.}$

${\displaystyle \mathbf {R} ^{+}\to \mathbf {R} ^{+}:x\mapsto x^{2}}$ , and thus also its inverse ${\displaystyle \mathbf {R} ^{+}\to \mathbf {R} ^{+}:10\mapsto {\sqrt {x}}.}$

The exponential function ${\displaystyle \exp \colon \mathbf {R} \to \mathbf {R} ^{+}:x\mapsto \mathrm {e} ^{ten}}$ (that is, the exponential part with its codomain restricted to its epitome), and thus as well its inverse the natural logarithm ${\displaystyle \ln \colon \mathbf {R} ^{+}\to \mathbf {R} :x\mapsto \ln {10}.}$

Injective and non-surjective

The exponential function ${\displaystyle \exp \colon \mathbf {R} \to \mathbf {R} :x\mapsto \mathrm {e} ^{x}.}$

Non-injective and surjective

${\displaystyle \mathbf {R} \to \mathbf {R} :x\mapsto (x-1)ten(ten+1)=x^{3}-10.}$

${\displaystyle \mathbf {R} \to [-i,ane]:x\mapsto \sin(ten).}$

Non-injective and non-surjective

${\displaystyle \mathbf {R} \to \mathbf {R} :ten\mapsto \sin(x).}$

Backdrop [edit]

• For every function f , subset X of the domain and subset Y of the codomain, X ⊂ f ⁻¹ (f(X)) and f(f ⁻ⁱ (Y)) ⊂ Y . If f is injective, so X = f ⁻¹ (f(X)), and if f is surjective, and so f(f ⁻¹ (Y)) = Y .
• For every function h : 10 → Y , 1 can define a surjection H : X → h(Ten) : 10 → h(10) and an injection I : h(X) → Y : y → y . Information technology follows that ${\displaystyle h=I\circ H}$ . This decomposition is unique up to isomorphism.

Category theory [edit]

In the category of sets, injections, surjections, and bijections correspond precisely to monomorphisms, epimorphisms, and isomorphisms, respectively.^[5]

History [edit]

The injective-surjective-bijective terminology (both as nouns and adjectives) was originally coined by the French Bourbaki group, earlier their widespread adoption.^[six]

See also [edit]

• Horizontal line examination
• Injective module
• Permutation

References [edit]

1. ^ ^{a b c d e f} "Injective, Surjective and Bijective". www.mathsisfun.com . Retrieved 2019-12-07 .
2. ^ ^{a b c d e f} "Bijection, Injection, And Surjection | Brilliant Math & Science Wiki". brilliant.org . Retrieved 2019-12-07 .
3. ^ ^{a b c d e f} Farlow, Southward. J. "Injections, Surjections, and Bijections" (PDF). math.umaine.edu . Retrieved 2019-12-06 .
4. ^ ^{a b c d e f} "6.3: Injections, Surjections, and Bijections". Mathematics LibreTexts. 2017-09-twenty. Retrieved 2019-12-07 .
5. ^ "Department 7.3 (00V5): Injective and surjective maps of presheaves—The Stacks projection". stacks.math.columbia.edu . Retrieved 2019-12-07 .
6. ^ Mashaal, Maurice (2006). Bourbaki. American Mathematical Soc. p. 106. ISBN978-0-8218-3967-6.

External links [edit]

• Earliest Uses of Some of the Words of Mathematics: entry on Injection, Surjection and Bijection has the history of Injection and related terms.

norrisyounnevernew68.blogspot.com

Source: https://en.wikipedia.org/wiki/Bijection,_injection_and_surjection

Share this post